Opis gry - Warcaby na urządzenia mobile i stacjonarne
Poniżej w skrócie przedstawiam zasady gry w warcaby, którymi kierowałem się pisząc swoją grę:
- pionek może poruszać się o jedno pole do przodu po przekątnej na wolne pole,
- pionek może bić zarówno do przodu, jak i do tyłu,
- damka może poruszać się w jednym ruchu o dowolną liczbę pól do przodu lub do tyłu po przekątnej i w trakcie swojego ruchu może zbić przeciwnika,
- bicia są obowiązkowe,
- wygrywa gracz, który zbije wszystkie pionki przeciwnika lub go zablokuje,
- w przypadku trzykrotnego powtórzenia ruchu gracza i przeciwnika następuje remis.
Przykładowe bicia dla pionka jak i damki pokazałem na poniższych rysunkach, za pomocą czerwonego krzyżyka pokazałem możliwe ruchy do wykonania przez komputer.
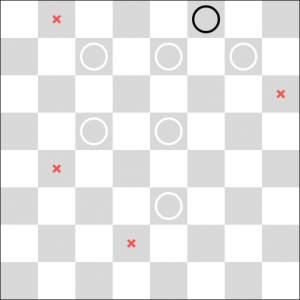
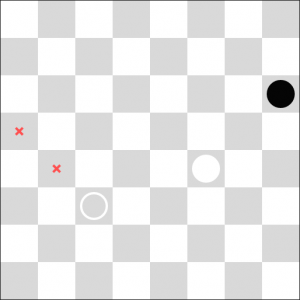
Gra została napisana w podobny sposób jak kółko i krzyżyk - patrz: Opis gry - zaawansowane kółko i krzyżyk na urządzenia mobile i stacjonarne. W warcabach także wykorzystałem algorytm: "Alpha-beta pruning" do wyznaczenia ruchów komputera. Największym wyzwaniem dla mnie, podczas pisania tej gry było zrealizowanie bicia pionkiem i damką. Poniżej przedstawiam funkcję, która zwraca wszystkie bicia zarówno pionka jak i damki (funkcja zwraca ścieżki od korzenia do wszystkich liści w drzewie, działa w sposób rekurencyjny).
function possibleBeatsMovePath(matrixIn, inn ,enemies, pathIn, pathLen, paths)
{
pathIn[pathLen] = inn;
pathLen++;
matrixIn[inn.beat_y][inn.beat_x] = blank;
var x = inn.x;
var y = inn.y;
var value = inn.value;
if( (draftsman_black === inn.value) || (draftsman_white === inn.value) ){
var out = possibleBeatsDraftsman( matrixIn, x, y, value, enemies );
}
if( (king_black === inn.value) || (king_white === inn.value) ){
var out = possibleBeatsKing( matrixIn, x, y, value, enemies, inn.beat_x, inn.beat_y );
}
if( !out.length ){
var beat = [];
for(var j=1; j<pathLen; j++ ){
beat.push(pathIn[j]);
}
if( !beat.length ){
return false;
}
var path = { 'x': x, 'y': y };
path.beats = [];
path.beats = beat;
paths.push( path );
return paths;
}
for (var ii in out){
paths = possibleBeatsMovePath(matrixIn, out[ii], enemies, pathIn, pathLen, paths);
}
return paths;
}
Gdzie funkcje: "possibleBeatsDraftsman" i "possibleBeatsKing" zwracają możliwe bicia dla współrzędnych x i y odpowiednio dla pionka i damki.
Natomiast funkcja oceniająca planszę, którą nazwałem 'evaluate' jest stosunkowo prosta i jest ona wykorzystana do wyznaczenia optymalnego ruchu komputera. Założyłem, że pionek gracza ma wartość 2 a damka 12, natomiast pionek komputera -2, a damka -12. Ocena planszy w mojej grze to suma:
- suma punktów pionków i damek,
- suma punktów pionków i damek jakie dany gracz bije,
- suma punktów pionków i damek jakie dany gracz straci ze znakiem przeciwnym.
Pionek, który znajduje się w pierwszym i drugim rzędzie oraz ostatnim i przedostatnim dostaje wiekszą ilość punktów.
Napisałem 63 testy jednostkowe przy pomocy mocha.js, które sprawdzają logikę gry. Aby wywołać np. test sprawdzający najlepszy ruch dla pierwszej planszy pokazanej powyżej należy wykonać polecenie:
./node_modules/mocha/bin/mocha -g 'getBestMatix testMatrix'
Zasymulowałem także w testach sytuację, gdzie komputer gra sam ze sobą. Test nazwałem: 'test comp vs comp'. Dla jednego gracza (gracz1) ustawiłem poziom zagnieżdżenia algorytmu "Alpha-beta pruning" na dwa, natomiast dla drugiego gracza (gracz2) zmieniałem ten poziom od jedynki do dwunastu. Za każdym razem gracz drugi rozpoczyna grę. Poniżej przedstawiam wynik moich testów:
| poziom zagnieżdzenia gracza 2-go | suma punków planszy końcowej | ocena planszy końcowej | wygrany |
|---|---|---|---|
| 1 | -28 | -298 | gracz1 |
| 2 | 16 | 171 | gracz2 |
| 3 | -- | -- | ruchy powtarzają się |
| 4 | -- | -- | ruchy powtarzają się |
| 5 | 20 | 212 | gracz2 |
| 6 | 16 | 164 | gracz2 |
| 7 | 18 | 186 | gracz2 |
| 8 | 20 | 211 | gracz2 |
| 9 | 28 | 285 | gracz2 |
| 10 | 28 | 284 | gracz2 |
| 11 | 20 | 210 | gracz2 |
| 12 | 6 | 66 | gracz2 |
Dla trzeciego i czwartego poziomu zagnieżdżenia gracza drugiego nie byłem w stanie ustalić sumy punktów i wygranego gracza, ponieważ ruchy graczy powtarzały się co cztery ruchy. Dla coraz większego poziomu zagnieżdżenia algorytmu "Alpha-beta pruning" gracz drugi wygrywa i jest to zachowanie zgodne z oczekiwaniem. Moim zdaniem bardzo ciężko jest wygrać z komputerem przy szóstym poziomie zagnieżdżenia algorytmu, jest to trzeci poziom w mojej grze.